月もリンゴもおんなじだ! 近代科学の父、ニュートンの大発見《宇宙一わかりやすい科学の教科書》

*この記事は、「ライティング・ゼミ」の上級コース「ライターズ倶楽部」にご参加のお客様に書いていただいたものです。
人生を変えるライティング教室「天狼院ライティング・ゼミ」〜なぜ受講生が書いた記事が次々にバズを起こせるのか?賞を取れるのか?プロも通うのか?〜
記事:増田 明(READING LIFE公認ライター)
今から350年ほど昔のこと、イングランドのある科学者が、当時としてはまったくありえない、突拍子もないことを言い出しました。
「実は月もリンゴも同じなんじゃない!?」
いったい何を言っているのでしょうか? 身近な果物のリンゴと、夜空に輝く月が同じとは?
そんなことを言い出した科学者の名前は「アイザック・ニュートン」。今では「近代科学の父」と言われる天才科学者です。
まあ、ニュートンは実際に「月とリンゴは同じ」と言ったわけではないのですが、このような意味のことを言ったのです。それはこんな内容でした。
月は約一ヶ月で地球の周りをぐるっと一周している。この「月が地球を回る現象」と「地上で物体が下に落ちる現象」、例えばリンゴが木から落ちるような現象は、実はまったく同じ原理で起こっているのだ!
この学説は今では「万有引力の法則」と呼ばれています。ニュートンは、リンゴが木から地面に落ちるのを見て、この着想を得たと言われています。
読者の皆さんは、もしかして理科の授業で「万有引力の法則」を習っていて、それほどおかしな話には聞こえないかもしれません。しかし当時の人達とっては、「何いってんの? ちょっと頭おかしいんじゃない?」と思うほど突拍子もないことでした。
普段当たり前に目にする「物体が落ちる」という現象と「空の月の動き」。あまりにもスケールが違いすぎて、見た目も違いすぎて、同じ原理で起こっている現象だなんて、とても思えなかったのです。
天と地の科学史
中世ヨーロッパでは、ギリシャの哲学者アリストテレスの考えが広く知られていました。
「物体が落ちる」という現象は、物体のあるべき場所が「地面」だからだ。物体はあるべき場所に戻ろうとするために落ちるのだ。
そう考えられていました。
そして、地球は宇宙の中心にあって、太陽や月や星々は、地球の周りを回っている。地上の物体と違って、決して地面に落ちてこないそれら天体は、地上の物体とはまったく別次元の存在で、まったく別の「天の法則」によって動いている、と考えられていました。
16世紀になると、天才科学者ガリレオ・ガリレイが、様々な実験を行って地上の物体の運動を研究しました。例えば以前は、「重い物体ほど早く落ちる」と言われていましたが、実際には「重い物体も軽い物体も同じ速度で落ちる」ということが分かりました。そして落下する物体の速度がどのように変化していくかなど、物体の運動について、いろいろなことが明らかになっていきました。
さらにガリレオは「望遠鏡」を発明し、天体を詳しく観測しました。そして、地球は宇宙の中心ではなく、火星や木星などの他の惑星と共に、太陽の周りを回っている、という地動説を唱えました。
その後、さらに天文学の研究が進んでいき、惑星がどのような軌道で太陽の周りを回っているか、次々と明らかになっていきました。特に、天文学者ヨハネス・ケプラーは、惑星の軌道と速度と公転周期(太陽を一周するのにかかる時間)に、規則性があることを発見し、それを「ケプラーの法則」としてまとめました。
天文学は華々しく進歩していき、人々の古い宇宙観はどんどん塗り替えられていきました。
しかし、どのように惑星が太陽の周りを回っているか、ということは分かってきましたが、なぜ惑星が太陽の周りを回るのか、その原理はよくわかっていませんでした。当時の科学者達は頭を悩ませ、いろいろな説を考えました。
例えば、宇宙空間が何か物質で満たされていて、太陽の周りでその物質が渦巻きを作っていて、その渦巻きの力で惑星が動いている、とする「渦動説」。太陽が磁石のように磁力を出していて、それが惑星を動かしている、とする「磁力説」もありました。しかしどの説も、矛盾なく惑星の運動を説明することはできませんでした。この問題は、長い間科学者達を悩ませました。
そんな中、天才科学者アイザック・ニュートンは、17世紀後半に、ある革命的な説を唱えました。それが「万有引力の法則」だったのです。
科学界の革命「万有引力の法則」
ニュートンは、「惑星が太陽の周りを回るのは、太陽が惑星を万有引力によって引っ張っているからだ」と考えました。
それまでの「渦動説」や「磁力説」と、ニュートンの「万有引力の法則」の最も大きな違いは、力の働く向きです。
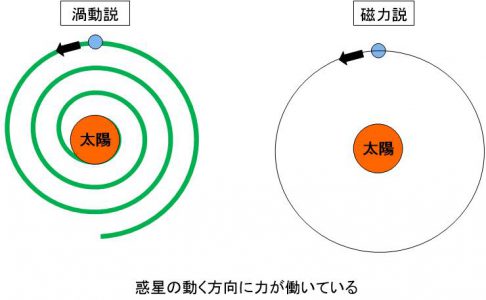
「渦動説」も「磁力説」も、惑星が動く方向に力が働いている、と考えていました。まあ、単純に考えればそうなりますよね。
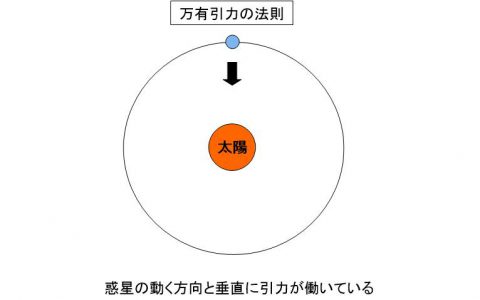
ところがニュートンは、惑星が進む方向ではなく、進む方向と垂直な、太陽の方向に力が働いている、と考えました。
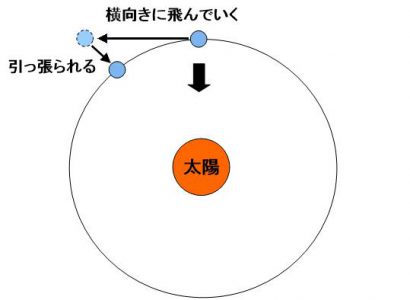
もし惑星を引っ張る力がなければ、円運動をしている惑星は、真っ直ぐ横向きに飛んでいってしまうはずだ。その惑星を太陽が引っ張り、惑星は太陽に向かっていわば「落下」する。この落下する動きと、横方向に飛んでいく動きが合わさって、惑星の軌道は曲がる。惑星は常に横方向に飛んでいきながら、太陽方向に落下し続け、それがちょうど合わさって円軌道を描いて、太陽の周りを回るのだ。
宇宙空間はほとんど真空なので、惑星の運動にブレーキをかけるものがない。そのため、「渦動説」のような横向きの力が働かなくても、一度動き出してしまえば、中心に向かう引力だけで、円運動はずっと続くのだ。
(太陽系が作られる過程で、回転力が働き惑星が動き出したと言われています)
さらにニュートンは、その太陽の引力の強さについて考えました。その時、考えの元になったのが、天文学者ヨハネス・ケプラーの作った「ケプラーの法則」でした。
ケプラーは、惑星の太陽からの距離と、惑星の公転周期(太陽を一周するのにかかる時間)の間に、規則性があることを発見しました。
太陽系には、いくつもの惑星があります。太陽からの距離が遠い惑星ほど、公転周期が長くなります。その距離と周期の関係が、不思議と規則的で、それを数式で表すことができました。それが「ケプラーの法則」でした。
太陽系の全ての惑星が、その法則に従っていました。ケプラーは観測によってその法則に気づいたのですが、なぜこんな規則性があるのかは、まったく分かっていませんでした。
ニュートンは「太陽が惑星を太陽方向に引っ張る」という考えを元に、ケプラーの法則を詳しく分析しました。すると次のことがわかったのです。
太陽の引力は、太陽からの距離が遠くなればなるほど弱くなる。例えば距離が2倍になると、力は1/2☓2、つまり1/4になる。距離が3倍になると、力は1/3☓3、つまり1/9になる。太陽の引力は「1/距離☓距離」に従って変化する。
これは「逆二乗の法則」と言われています。
「太陽が惑星を太陽方向に引っ張る」ということ、その力の強さが「逆二乗の法則」に従うということ、この二つが正しければ、そこから数学的な計算で「ケプラーの法則」を導き出すことができる。
そうニュートンは言い、実際に「ケプラーの法則」を導き出しました。
発見したケプラー自身が、なぜこんな法則が成り立っているのかわからなかったものを、ニュートンはシンプルな二つの規則から、見事に説明してしまったのです。
さらにニュートンの快進撃は続きます。
月もリンゴもおんなじだ
太陽が惑星を引っ張る力は、実は太陽だけのものではない。地球も同じ力で、月を引っ張っているのではないか。だから月は地球の周りを回っているのではないか。
そして科学の歴史をひっくり返し、人々の世界観を一変させた驚愕の考えに至ったのです。
地上で物体を落下させている力も、同じ力なのではないか?
ニュートンはそのことを証明しようとしました。
当時、月と地球の距離が約38万km、ということは観測で分かっていました。又、地球の半径は約6300km、ということも分かっていました。
それらのことから、地球が月を引っ張る引力がどのくらいかを、理論的に計算したのです。
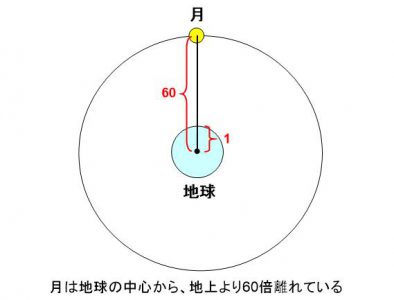
地球の中心から引力が発生しているとすると、地上の物体は、引力の発生源から地球の半径分、つまり6300km離れていることになります。月は、引力の発生源から地球と月の距離分、つまり38万km離れていることになります。
そうすると、月は地上の物体に比べて、引力の発生源から、約60倍(38万÷6300)離れている、ということになります。
そうなると、「引力は1/距離☓距離に従って変化する」という「逆二乗の法則」から、月が地球に引っ張られる力は、地上の物体が地球に引っ張られる力よりも、1/60☓60 つまり3600分の1になるはずです。
月は、地上の物体の3600分の1の力で引っ張られ、地球に向かって「落下」していることになります。
一方、地上で物体を落とすと、どんな重さの物体でも、最初の1秒間で約490cm落下する、ということが分かっていました。
地上の物体に比べて、月は3600分の1の弱い力で、地球に引っ張られています。月が地球に向かって「落下」しているとすると、その弱まった分だけ、月の「落下距離」は短くなるはずです。
理論的には、1秒間で月が落下する距離は、地上の物体の落下距離に3600分の1をかけて、490/3600cmになるはずです。
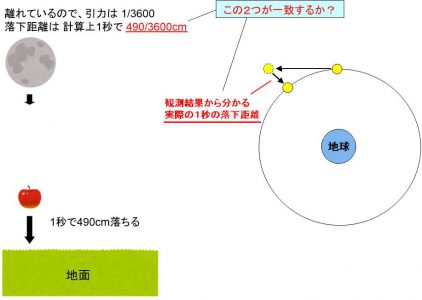
実際はどうなのでしょうか? 実際の月の落下距離はいくつなのでしょうか?
月が実際にどんな軌道を描いているかは、観測で分かっていました。月が地球に向かってどのくらい落下していれば、現実の月の軌道になるかは、観測結果から簡単な計算で求められます。
そうやって求めた実際の落下距離と、理論的な計算結果を比較し、一致していたら、ニュートンの「万有引力の法則」は正しいことになります。
比較した結果、二つの値は本当に一致しました。理論的な計算結果も、実際の観測結果から求めた値も、どちらも月の落下距離は「1秒間に約490/3600cm」だったのです。理論的な計算結果と現実の値が一致したのです。つまり「万有引力の法則」は真実だったのです。
ついに、「地上の物体の落下運動」と「月が地球を回る運動」が同じ力によるものだということが、科学的に明らかにされたのです。
「万有引力の法則」が近代科学に与えた意味
「万有引力の法則」の発見は、天と地をつなぐ、歴史的な大発見でした。長い間、天体は地上の物とはまったく別の存在だと考えられていました。別次元の神聖な「天の法則」で動いている、そう思われていました。「天の法則」は、長い間謎に包まれていました。
しかしその「天の法則」は、実は地上の法則とまったく同じだったのです。天の月の動きも、地上のリンゴの動きも、まったく同じことだったのです。
この「一見まったく別に見える現象が、実は同じ法則で説明できる」ということ、これこそが科学の最大の醍醐味であり、最大の強みであり、これを目指すことが、科学の大きな目標なのです。
20世紀になると、天才物理学者アルバート・アインシュタインが、「万有引力の法則」を超える新しい引力理論「一般相対性理論」を作り上げました。それによって、ニュートンの万有引力の法則は書き換えられました。万有引力の法則でも、惑星の動きをほとんど正確に説明できるのですが、一般相対性理論のほうがより正確だったのです。
しかし万有引力の法則が書き換えられた今でも、ニュートンは「近代科学の父」と呼ばれ、科学者たちの尊敬を集め続けています。
それは、
「一見複雑に見えるこの世界の様々な現象が、実はシンプルな法則で繋がり、美しく調和している。その調和を、実験や数学を通して解き明かしていく。それが科学である」という、近代科学の大きな方向性を決定づけたのが、ニュートンの発見だったからなのではないでしょうか。
【参考文献】
「プリンキピアを読む」和田純夫 講談社
❏ライタープロフィール:増田 明
神奈川県横浜市出身。上智大学理工学部物理学科卒業。同大学院物理学専攻修士課程修了。同大学院電気電子工学専攻修士課程修了。
大手オフィス機器メーカでプリンタやプロジェクタの研究開発に従事。父は数学者、母は理科教師という理系一家に生まれる。子供の頃から科学好きで、絵本代わりに図鑑を読んで育つ。
学生時代の塾講師アルバイトや、大学院時代の学生指導の経験から、難しい話をわかりやすく説明するスキルを身につける。そのスキルと豊富な科学知識を活かし、難しい科学ネタを誰にでもわかりやすく紹介する記事を得意とする。
この記事は、天狼院書店の大人気講座・人生を変えるライティング教室「ライティング・ゼミ」の上級コース「ライターズ倶楽部」にご参加のお客様が書いたものです。ライティング・ゼミにご参加いただくと記事を投稿いただき、編集部のフィードバックが得られます。チェックをし、Web天狼院書店に掲載レベルを満たしている場合は、Web天狼院書店にアップされます。
人生を変えるライティング教室「天狼院ライティング・ゼミ」〜なぜ受講生が書いた記事が次々にバズを起こせるのか?賞を取れるのか?プロも通うのか?〜
お問い合わせ
■メールでのお問い合わせ:お問い合せフォーム
■各店舗へのお問い合わせ
*天狼院公式Facebookページでは様々な情報を配信しております。下のボックス内で「いいね!」をしていただくだけでイベント情報や記事更新の情報、Facebookページオリジナルコンテンツがご覧いただけるようになります。
■天狼院書店「東京天狼院」
〒171-0022 東京都豊島区南池袋3-24-16 2F
TEL:03-6914-3618/FAX:03-6914-0168
営業時間:
平日 12:00〜22:00/土日祝 10:00〜22:00
*定休日:木曜日(イベント時臨時営業)
■天狼院書店「福岡天狼院」
〒810-0021 福岡県福岡市中央区今泉1-9-12 ハイツ三笠2階
TEL:092-518-7435/FAX:092-518-4149
営業時間:
平日 12:00〜22:00/土日祝 10:00〜22:00
■天狼院書店「京都天狼院」
〒605-0805 京都府京都市東山区博多町112-5
TEL:075-708-3930/FAX:075-708-3931
営業時間:10:00〜22:00
■天狼院書店「Esola池袋店 STYLE for Biz」
〒171-0021 東京都豊島区西池袋1-12-1 Esola池袋2F
営業時間:10:30〜21:30
TEL:03-6914-0167/FAX:03-6914-0168
■天狼院書店「プレイアトレ土浦店」
〒300-0035 茨城県土浦市有明町1-30 プレイアトレ土浦2F
営業時間:9:00~22:00
TEL:029-897-3325








