この世界を支配する美しき法則「フラクタル」《宇宙一わかりやすい科学の教科書》

*この記事は、ライティング・ゼミをご受講いただいた方が書いた記事です。
【間もなく開講!】人生を変えるライティング教室「天狼院ライティング・ゼミ」〜なぜ受講生が書いた記事が次々にバズを起こせるのか?賞を取れるのか?プロも通うのか?〜《全国通信受講対応》
記事:増田 明(READING LIFE公認ライター)
今回は、この世界を支配するある「法則」についての話をします。この「法則」が発見されたのは1970年代のこと。長い人類の歴史の中ではごく最近と言っていいでしょう。長い間、世界を支配するこの「法則」に、人類は気がついていませんでした。
いや、実はなんとなくは気がついていたのかもしれません。はっきりと科学的には発見されていなかった、というだけかもしれません。
その法則は「フラクタル」と呼ばれています。「フラクタル」とはいったいなんでしょうか?
下に並んだ図形を見てください。一番左側はただのシンプルな三角形です。この三角形の各辺の真ん中に、少し小さな三角形を付け加えます。すると二番目のような星の形ができます。その星の各辺の真ん中に、さらに小さな三角形を付け加えます。すると三番目のコンペイトウのような形になります。さらにその各辺に三角形を作って……と繰り返していくと、どんどん細かい図形になっていき、雪の結晶のようなキレイな図形が出来上がります。
この図形は、どの部分をどの縮尺で見ても三角形で作られていて、拡大しても縮小しても同じ三角形が繰り返し規則的に現れます。このように、縮尺を変えてもいつまでも同じ形が規則的に続いていく図形を「フラクタル」と言います。この「フラクタル」が世界を支配している「法則」なのです。
フラクタルの発見
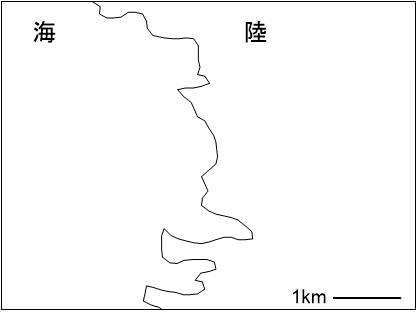
きっかけは「海岸線の長さ」についての数学の研究からでした。ごく普通の「海岸線の長さ」を測ろうとすると、ある奇妙な問題に突き当たってしまうのです。例えば、下の地図の海岸線の長さはどのくらいだと思いますか?
右下にある1kmの縮尺から考えると、だいたい5kmくらいでしょうか? 入り組んでいるからもう少し長くなって7kmくらいかもしれませんね。
さて正解はと言うと、この海岸線の長さは「無限大」です。
は? どういうこと? 長さが無限大なんてありえないでしょ!
と思うかもしれません。しかしこの海岸線は、間違いなく無限の長さを持っているのです。どういうことでしょうか?
海岸線のようにデコボコした物の長さを測るときは、モノサシの長さと、それを使ってどのように測るかが重要になってきます。例えば下図の左側のように、1km単位のモノサシで海岸線の長さを測ってみます。モノサシが5本分ですので、1km☓5=5kmです。ただモノサシが大きいので、海岸が入り組んでいる箇所は測れていません。
もうちょっと正確に測るために、図の右側のように、半分の0.5kmのモノサシを使ってみます。
これで測るとモノサシ16本分になりました。0.5km☓16=8kmです。先ほどより3km長くなりましたね。モノサシが細かくなったので、海岸線が入り組んでいる箇所も正確に測れたためです。じゃあこの海岸線の長さは8kmで決まりでしょうか? いや、そうとは言えません。さらにモノサシを細かくして海岸線にピッタリ沿うように測ると、さらに長くなってしまいます。
それだけではありません。地図を拡大していくと、見えていなかった細かい海岸線のデコボコがさらに見えてきます。それをもっと小さいモノサシで正確に測ると、さらに長さが伸びます。
地図を拡大し、細かいデコボコが見えてくるたびに、海岸線の長さは長くなります。地図では拡大に限りがありますが、実際の海岸線だったら、石ころ1つレベル、さらに砂粒1つレベルまで拡大できます。やろうと思えばさらに細かく、いくらでも拡大していくことができます。それを測っていくと、長さは果てしなくのびていき、ほぼ無限大になってしまうのです。
数学の世界で、それまで扱われてきた形、例えば円や三角形、四角形、六角形、などは、長さをはっきりと測ることができます。しかし人工的ではない自然界のものは、長さを測る、という一見単純なことがなかなかできないのです。
フランスの数学者、ベノア・マンデルブローは1970年代に発表した論文で、海岸線の長さを例に、このような自然界の形についての新しい考え方を提唱しました。
それまで数学で扱っていたような、三角形や四角形などの単純な形ではない、複雑な自然界の形。長さを測ることもままならない、一見とらえどころのない、でたらめな形のように見えます。しかし、マンデルブローはこの一見でたらめな自然界の形に、ある法則があることを発見します。
マンデルブローは海岸線のデコボコ具合が、地図の縮尺によってどのように変化するかを調べました。地図の縮尺を段階的に変えながら、海岸線の長さを測っていったのです。海岸線の長さは、デコボコ具合が大きければ大きいほど、長くなります。デコボコ具合が小さくなめらかなものほど、短くなります。海岸線の長さがデコボコ具合を表す数学的な基準となるのです。
そのように海岸線のデコボコ具合を詳しく調べていくと、どの縮尺だろうとデコボコ具合がほぼピッタリ同じになる、ということがわかったのです。どういうことか、実際の地図を例に説明していきましょう。
一番左側の地図の海岸線の一部を拡大してみます。その拡大した地図の一部をさらに拡大してみます。なんだか拡大しても似たような形が続いていくと思いませんか? 完全に同じ形ではありませんが、似たような形の、同じようなデコボコ具合の地図がいつまでも続いていくのです。デコボコ具合がほとんど同じなので、どのくらいの縮尺の地図なのかは、形を見ただけではよくわかりません。
この海岸線だけが、偶然そうなっているわけではありません。世界中の様々な海岸線を調べてみても、同じ結果になります。様々な海岸線はどれも、拡大しても縮小しても、デコボコ具合がほとんど同じなのです。縮尺をいくら変えても、同じような形がいつまでも続いていくのです。ある縮尺ではなめらかで、拡大するとデコボコになり、さらに拡大するとなめらかに戻り、というような、縮尺でデコボコ具合が変わる海岸線はほとんどなかったのです。
マンデルブローは、この海岸線の性質は自然界に普遍的な性質ではないか、と考えました。そしてそのような形を扱うための、新たな数学理論を構築していきました。それが「フラクタル」なのです。
世界中にひそむフラクタル
研究が進むにつれて、この性質は海岸線だけではなく自然界の様々なところに現れることがわかりました。例えば、樹木の枝分かれの形や、植物の葉の形、雲の形、山の起伏、雪の結晶の形なども、フラクタル構造を持っていました。人体の血管構造も同じで、拡大していくと同じような血管の枝分かれ構造が、繰り返し現れるのです。大きなものから小さなものまで、自然界のあらゆるところにフラクタル構造が現れていました。
例えば、このロマネスコというカリフラワーの一種なんか、わざとらしいくらいにフラクタルな形をしています。
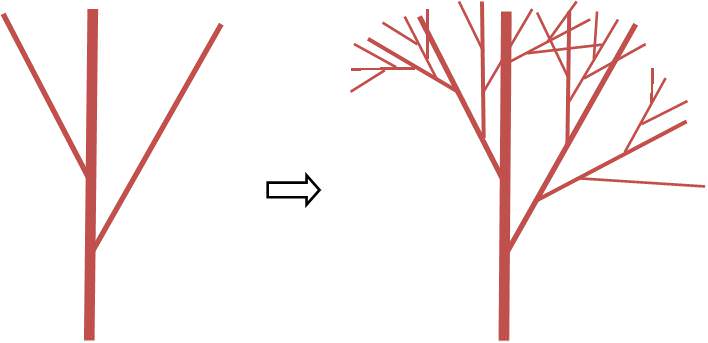
自然界がフラクタル構造を持っているということは、逆にフラクタルになるように図形を描いていけば、人工的に自然に近い形を作ることができます。例えば下の絵のように、単純な三本の線の組み合わせを、縮尺を変えて繰り返していくことで、樹木のような図形を描くことができます。
下の雪の結晶のような絵も、三角形を縮尺を変えて規則的に繰り返していくことで描かれています。
このように単純な形を規則的に繰り返していくことで、きれいに自然物を再現することができます。これはコンピュータグラフィックスなどに応用されています。
美しく調和した「フラクタルな世界」
1970年代、マンデルブローによってフラクタル理論が作られ、この世界に様々なフラクタルがあることがわかりました。それは驚くべき大発見でした。しかし人々は、この発見に驚くと同時に、深い納得感もまた感じていました。
数学的なフラクタルの概念が作られたのは、近年のことですが、フラクタルに似たものは、古くから芸術や宗教の世界に度々現れていました。例えば仏教には「マンダラ」と呼ばれる絵があります。
マンダラは世界全体の姿を描いていると言われています。そして、それは綺麗なフラクタル構造を持っているのです。仏教だけでなく、世界中の様々な美術や建築に、フラクタル構造が見られます。
全体と部分は同じであり、それが繰り返され世界が作られている。全体と部分は調和し、全体の中に部分があり、部分の中にまた全体がある。
近代科学の発展するはるか昔から、人々はそのような美しい調和が、この世界の本質であることを自然と見抜き、表現し続けてきたのではないでしょうか。
【参考文献】
「複雑系入門」井庭崇 福原義久 NTT出版
「フラクタル」高安秀樹 朝倉書店
❏ライタープロフィール
増田 明(READING LIFE公認ライター)
神奈川県横浜市出身。上智大学理工学部物理学科卒業。同大学院物理学専攻修士課程修了。同大学院電気電子工学専攻修士課程修了。
大手オフィス機器メーカでプリンタやプロジェクタの研究開発に従事。父は数学者、母は理科教師という理系一家に生まれる。子供の頃から科学好きで、絵本代わりに図鑑を読んで育つ。
学生時代の塾講師アルバイトや、大学院時代の学生指導の経験から、難しい話をわかりやすく説明するスキルを身につける。そのスキルと豊富な科学知識を活かし、難しい科学ネタを誰にでもわかりやすく紹介する記事を得意とする。
この記事は、天狼院書店の大人気講座・人生を変えるライティング教室「ライティング・ゼミ」を受講した方が書いたものです。ライティング・ゼミにご参加いただくと記事を投稿いただき、編集部のフィードバックが得られます。チェックをし、Web天狼院書店に掲載レベルを満たしている場合は、Web天狼院書店にアップされます。
【お申し込み受付中!】ライティング・ゼミについてはこちら↓
【間もなく開講!】人生を変えるライティング教室「天狼院ライティング・ゼミ」〜なぜ受講生が書いた記事が次々にバズを起こせるのか?賞を取れるのか?プロも通うのか?〜《全国通信受講対応》