1.ありがとう、位置情報 〜連立方程式〜《オトナのための中学数学》

記事:吉田健介(READING LIFE編集部公認ライター)
私が住んでいる京都は、連日多くの訪問客で賑わっている。
街を歩くと、国内の人だけでなく、外国人もたくさん見かける。
数年前までは、「外国人の人も増えたねー」と言い合っていたのだが、最近ではそれも珍しく無くなっている。
日本語以外の言語が飛び交っているのも、今や違和感はない。場所によっては、外国人の方が多いのではないか、と思うことも。お店によっては、「ここは外国か?」と錯覚することすらある。それくらい京都は、たくさんの外国人が往来し、京都の街並み、観光名所を巡っている。
初めて行く場所は不安も多い。地理は当然詳しくないわけで、駅から降りて、自分が今どの方向に向いているのか、分からなくなることもしばしばある。目的地へ向けてどの道をどのように進めば良いのか、観光ガイドに付いている地図だけでは難しい所。
そこで登場するのがスマホである。スマホに内蔵されている地図アプリ。これを駆使して、私たちは初めての場所でも、迷うことなく、方向感覚が狂わされずに、ゴールへ到達することが可能だ。
京都の街で、スマホを片手に歩いている観光客は多い。最近では、車の運転でも活用している。ナビは必要ない。スマホ一台で十分事足りてしまうわけだ。
自分が現在どこにいるのか、そしてどの方向を向いているのか、地図アプリを通して、敏感に画面に表示してくれる。歩き出すと、その速度に合わせて、地図上の現在地も移動する。方向転換をすると、画面上でも、方向転換をしてくれる。目的地までどのくらいかかるか、どのルートを辿るべきか、全て表示してくれる。
右に曲がり損ねても
「ちょっとちょっと、違うって、もう! さっきの角を曲がるの!」
と叱られることはない。
さりげなく、スマートに、静かに、別ルートを紹介してれる。決して叱責されることはない。優しさすら感じる。
この地図アプリ、一体全体、どういった仕組みで現在地を割り出しているか、考えたことはあるだろうか。
「どうやって? そりゃ、衛星から場所をキャッチしてくれてるんでしょうよ」
概ねそういったイメージではないだろうか。
正解である。
スマホに内蔵されている、GPSを衛星がキャッチして現在地を割り出しているのだ。
ただその仕組みに、ある計算が使われていることは、意外と知られていない。
「こんなの役に立つの?」
「世の中に出ても使わねーし」
「なくても生きていけるって」
中学生の頃、一度は口にしたセリフ。そしてこのセリフを浴びせられやすい数学の単元。
特に悪意はないのだが、ついつい八つ当たりされてしまう計算。
それは、連立方程式である。
実はこのGPS、現在地を探知するために、連立方程式が使われているのだ。
「へーそうなんだ」と思ったあなた。ありがとう。そうなんです。
GPS
グローバル・ポジショニング・システム
地球上のどこにいるのかを測定してくれるシステムだ。
このGPSは、自分の場所を示してくれる印となっている。
下の問題を見てほしい。
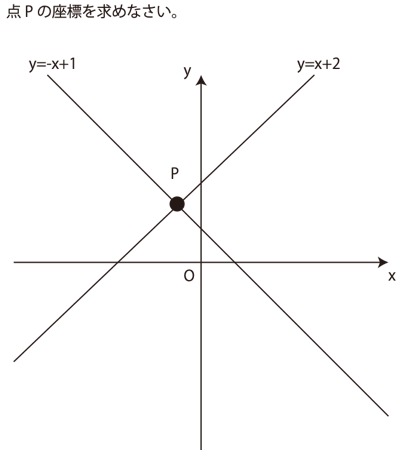
これは、中学校で登場する問題だ。
2本の直線から、印の付いた座標を求める問題。
言い換えると、2つのヒントから、場所を特定すること。
これを解くためには、2直線を連立方程式する必要がある。
つまり連立方程式は、場所を特定、探知するための道具なのだ。
もう少し詳しく見ていく。
地球の周りを飛ぶ衛星は、四方八方に電波を飛ばしている。
大きな球体をイメージしてもらうとよい。
この衛星、私たちのスマホを見つけると、電波を広げてスマホと繋げてくれる。
ただ、1つだけではうまく場所を特定することはできない。どうしても誤差が出てきてしまう。最低でも3つを使用する(実際には4つ使われているそうだ)。
イメージしてほしい。
3つの衛星が、1台のスマホめがけて場所を特定する。すると、円が重なる所が出てくる。この重なりを使って、詳しい場所を絞っているのだ。
舞台に立つキャストを3方向からスポットライトで当てているのと同じだ。
3つのスポットが重なる所が、一番明るくなるはず。位置情報も同じ原理というわけだ。
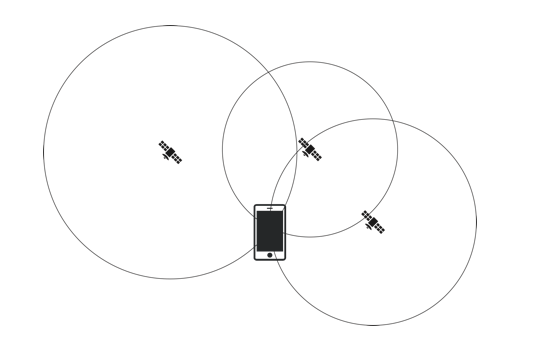
スマホの位置を仮に、( x , y , z ) と仮定。
衛星1つにつき、( x , y , z ) を使って式を作る。
「だいたいこの辺かなー」という具合の式だ。
衛星が3つあるので、式が3つ完成する。
「だいたいこの辺かなー」
「俺はこの辺りだと思う」
「私はここにいると予測!」
3つの意見をすり合わせ、つまり連立方程式すると、より正確な位置を絞ることができる。
スマホの画面が、詳しく自分の位置を教えてくれるのは、こうした理由があるというわけだ。
たまに誤作動で、画面上では建物の上を歩いていたら、誰かが計算間違いでもしたのかな、と温かい目で見てほしい。
こうして連立方程式は、場所を特定するための道具として、私たちの見えないところでフル活動しているわけだ。
他にも、位置情報を特定するために使われる場面がある。
それはミサイルの迎撃。
発射されたミサイルを撃ち落とす方法として、連立方程式が使われる。
下図のような放物線と直線をイメージしてほしい。
このようにして、場所を予測し、狙った場所で撃ち落とすことができるわけだ。
ただ、そんな場面は現実になってほしくないが。
世の中のどのような場面で使われているのか。具体的な場面を知ることで、少し見え方が変わってくるのではないだろうか。
「やるじゃん、連立方程式」
見直してくれる人がいるかもしれない。
ちょっと感謝してくれる人も中にはいるかもしれない。
ありがとう、連立方程式。
これからもよろしく、連立方程式。
❏ライタープロフィール
吉田 健介(READING LIFE 編集部公認ライター)
現役の中学校教師。教師が一方的に話をするのではなく、生徒同士が話し合いながら課題を解決していく対話型の授業を行なっている。様々な研究授業で自らの授業を公開。生徒が能動的に学習できるような授業づくりを目指している。
この記事は、天狼院書店の大人気講座・人生を変えるライティング教室「ライティング・ゼミ」を受講した方が書いたものです。ライティング・ゼミにご参加いただくと記事を投稿いただき、編集部のフィードバックが得られます。チェックをし、Web天狼院書店に掲載レベルを満たしている場合は、Web天狼院書店にアップされます。
http://tenro-in.com/zemi/103447



