3. 平面図形に乾杯〜六角形〜 《オトナのための中学数学》

記事:吉田健介(READING LIFE編集部公認ライター)
三角形、四角形、五角形、六角形……
いわゆる平面図形というものは、私たちに馴染みのあるものたちであり、身近な存在である。
「何にどう使われているかって? そりゃ色々な所に使われているよ。例えば三角形は……」
それぞれの形が、周りの世界にどう使われているか、どのように活用され、どう関わっているか。目に見える形、見えない形。
突然「図形って、何に使われているの?」と聞かれたとしても、比較的答えやすいのではないだろうか。それ程、図形というものは私たちと一緒に毎日を過ごし、お互いよろしくご機嫌で支え合っている仲だと言える。
普段使用している道具や家具、建築といった、形として存在するもの。
デザインや模様といった、目を楽しませてくれるもの。
コンピューターゲームやCGアニメーションなど、設計で使用される理論的なもの。
活躍の場は様々だ。知れば知るほど「へー、そんな所にも使われているんだね」となる。
私たちが生活の場へと活用させているのと同時に、自然界にも図形は存在する。
「自然の中で、図形になっているものって何?」
そう聞かれると、あなたはまず何を思い浮かべるだろうか。
街を歩いていて、いきなりそんな質問をされることはないだろう。
例えば、たまたま電車で親子の会話が聞こえてきたとする。
「ねえねえお母さん、自然の中に図形ってあるの?」
周りからすれば、なんて知的な質問なんだボーイ、と関心するかもしれない。
あくまで例え話。
仮にそんな会話が聞こえてきたとき、あなたは心の中で何と答えるだろうか。
おそらく、このタイプの質問で上位に食い込んでくる図形が六角形ではないだろうか。
三角形でも四角形でもない。六角形。
なぜなら、「蜂の巣」と繋がるからだ。
広く知られている通り、蜂の巣は六角形をしている。
「そうねー、蜂さんのお家ね」
母親が穏やかな目で答える。子供の純粋な質問に優しく回答する。
「あ、そっかー」
周りの空気もどこか和む。微笑ましい光景。
見ている私たちも、母親と似たような気持ちに包まれる。
子供の知的探究心に、温かい気持ちになる。
「何で六角形なの?」
そこで終わっていればよかったものの、彼の探究心は終わらない。
「何で? 何でってー……」
さて困った。自然界にある図形の代表、蜂の巣の六角形。
すぐに思いつきやすいものである。「京都と言えば、お寺」というくらい、レギュラーな回答だ。
だが、更に突っ込んで、「なぜ六角形なのか」という問いに対して、果たしてどのくらいの人が答えることができるだろうか。
テレビやインターネットなど、何かしらのどこかしらで、この「なぜ六角形」問題は解決されてきた問いでもある。ポケットからスマホを取り出して調べても、すぐに答えに行き着くだろう。しかしここは格好よく、ノーカンぺで答えることが出来たら、格好よくないだろうか。
子供の無邪気な質問に、周りの空気は和んでいた。
だが、「何で?」と突っ込まれた瞬間、視線は母親に集中する。瞬間的に、何かを測るかのような視線が、静かに母親に注がれる。
今日は、そんな変化球に対して、真っ向からキャッチできるようになるためのお話。
「いや、そんな機会滅多にないって」
まあ、そう言わないで。変化の激しい世の中、何が起こるか分からない。
そんな小さな想定も時に必要になるかもしれない。ほんの小さなメモ程度の知識。ノートの端にパラパラ漫画を描くような気分で、小さく細やかに納得する話。たまにはそんな話もいいんじゃないでしょうか。
実験をしてみよう。
図のように、円、正三角形、正方形、正五角形、正六角形の5つを考える。
単純にそれぞれを敷き詰めた場合、このような状態になる。
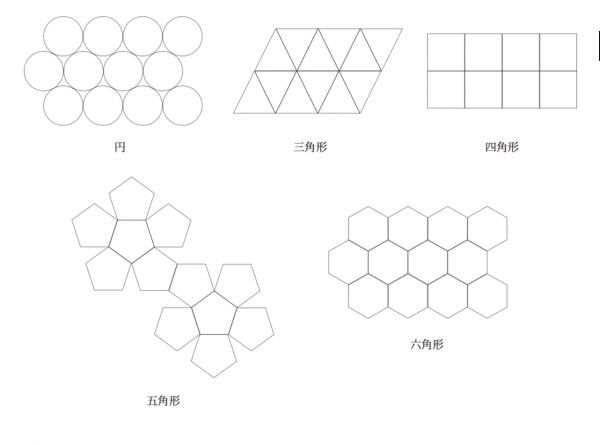
すき間を見て欲しい。
円と五角形以外は、すき間なく敷き詰めることができている。
このすき間がない、というのは重要である。
もしすき間がたくさんあった場合、蜂の子どもが落っこちてしまう。
「いやいや、落っこちるほどのすき間なんてできないって」
「働き蜂の働きっぷりを舐めてもらっては困るね」
そう言われるかもしない。だが大なり小なり、隣にすき間が空いているのは具合がよろしくない。
仮にリビングと寝室へ行く間にすき間があったらたまったもんじゃない。
マンションなら、下の人が歯を磨きながらテレビの前で爆笑しているのが丸見えである。
それはそれで微笑ましい光景かもしれないが…… とにかく、嫌だ。そう、嫌だ。
ましてや、すき間があるということは、安定感にも乏しい。
風が吹くとグラグラ揺れ、子供が走り回るとどんどん傾く。たまったもんじゃない。
なぜ、三角形、四角形、六角形の3つは隙間ができないかと言うとと、下図の通りだ。
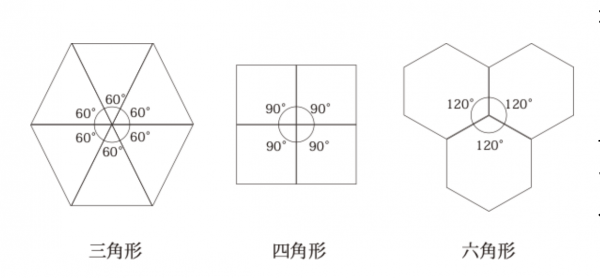
敷き詰めた部分の角度を見ると、全て360度になっている。
すき間なく敷き詰めることができる条件として、この360度が前提になるのだ。
そのためには、1つあたりの角度がポイントとなるわけだ。
円や五角形はその条件を満たしていない。集めても360度にならないのだ。だから綺麗に敷き詰めることができない。
ちなみに、この敷き詰め条件を満たすことができる平面図形はこの3つだけだ。すき間がある、というのは、集団生活をする蜂にとって、あまりよろしくない構造なのである。
もう少し話を進めてみよう。面積に注目してみる。
1辺が1センチだとすると、それぞれの面積は次のようになる。
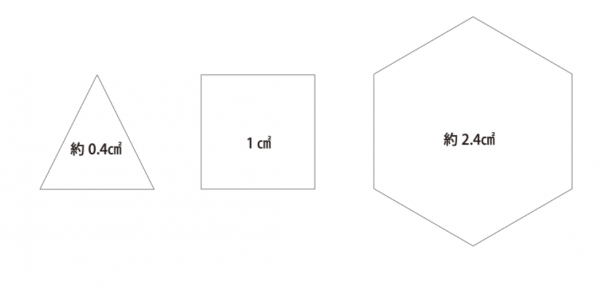
なんと、六角形の面積が一番大きくなることだ。
広々、ゆったり、快適。
部屋を作るには持ってこい。あくまで蜂にとって。
私たちならば、三角形や四角形の部屋なんて、デザインによってはありうるかもしれない。
だが、蜂にとっては六角形が最も具合が良いのだ。
この、六角形を並べたものをハニカム構造という。構造的にとても丈夫なのだ。飛行機や人工衛星などにも使用されている。
広さが最大限、強度は申し分ない。
これが蜂の巣が六角形である所以だ。
もしかしたら昔の蜂は、「いや四角形っしょ!」となったファミリーもいたかもしれない。
その辺り、理由は定かではないが、どこかしら何かしらで失敗と成功を繰り返し、今に至っているに違いない。想像だ。
「すき間なく並べることができるからよ。しかも六角形が一番広くなるの」
「へー!」
周りで聞いていた人は驚くはずだ。
事もなげに、自然に答える母親の姿に関心するはず。
世の中には多くの図形が存在している。
私たちの生活と自然界と。
使われ方は様々だが、その理由を知ることで、世界が深まったような気持ち良さがある。
完成したパラパラ漫画を眺めるような、小さな幸せ。
今日はそんなちょっとしたサイドメニューなお話。
六角形の話。
平面図形に乾杯。
❏ライタープロフィール
吉田 健介(READING LIFE 編集部公認ライター)
現役の中学校教師。教師が一方的に話をするのではなく、生徒同士が話し合いながら課題を解決していく対話型の授業を行なっている。様々な研究授業で自らの授業を公開。生徒が能動的に学習できるような授業づくりを目指している。
この記事は、天狼院書店の大人気講座・人生を変えるライティング教室「ライティング・ゼミ」を受講した方が書いたものです。ライティング・ゼミにご参加いただくと記事を投稿いただき、編集部のフィードバックが得られます。チェックをし、Web天狼院書店に掲載レベルを満たしている場合は、Web天狼院書店にアップされます。
★10月末まで10%OFF!【2022年12月開講】人生を変えるライティング教室「天狼院ライティング・ゼミ《土曜コース》」



