5. そんな所に君の存在〜素数〜 《オトナのための中学数学》

記事:吉田健介(READING LIFE編集部公認ライター)
さて、想像してほしい。
今あなたは新幹線の中にいる。車両への自動扉が開き、「さてどこに座ろうか」と手頃な座席を探している。
車両に沿って真っ直ぐに伸びた通路。
両サイドには座席のシートが並び、すでに乗っている乗客の頭がポツポツと見える。
スーツを着たサラリーマン2人組。上司らしい人はスマホを眺めている。部下っぽい人は、ノートPCを広げて、カタカタとキーボードを鳴らしている。
おしゃべりをするマダム3人組の姿も見える。温泉旅行にでも行くのだろうか。お菓子をつまみながら、楽しそに話をしている。
外国人の姿も見える。大きなリュックが荷物棚に置かれている。次の目的地へと向かっているのかもしれない。
「できたら窓際がいいな」
そんなことを考えながら、あなたは手頃な座席を探す。
1つ向こうの車両には、修学旅行生でもいるのだろうか。トイレの前に並ぶ制服姿の学生たちが、目に入る。
みんなそれぞれの目的に向けて、各々の時間を過ごしている。
新幹線。
少し特別な気分になる乗り物。
時速300kmという乗り物は、不思議と気分をワクワクさせてくれる。
ではここで問題。
新幹線の座席、何列シートになっているか分かるだろうか。
よく新幹線を利用する人ならすぐに思い浮かぶだろう。
わからない人は、何列なのか少し考えてみてほしい。
正解は、2列と3列。
グリーン車は2列のみだが、今は自由席を想像してほしい。
1両あたり100名程乗ることができ、シートは2列3列と左右の数が違う。
では、さらに質問。なぜ、2列と3列になっているのだろうか。
なぜ?
「なぜって…… 理由あるの?」
そう思うかもしれない。理由は、ある。
デザイン的な理由、構造上の理由、そういったものではない。
ちゃんと、2列と3列でなければいけない理由が存在する。
「へー、そうなんだ。考えたこともないや」
そう、ほとんどの人は考えたこともないかもしれない。
日本人がなぜ白飯を食べているのか、という程、当たり前のことであり、自然なことであり、自然過ぎて、その理由すら考えたこともない人がほとんどかもしれない。
しかしあるのだ、明確な理由が。
「ほうほう、是非知りたいね」
これには数学的な観点で説明することができる。
2と3。ポイントはこの2つの数字だ。
1や4ではいけない。
2と3でなければいけない。
焼き肉に白ごはんが必須なように、そうでなければならない理由がある。絶対的な理由。
それは、2列と3列なら、どんな団体客でも対応できるからだ。
「ん? どういうこと?」
そう思った人は、今の意味を噛み砕いて考えてみてほしい。
自分で更に分析したい人は、コーヒーでもいれて、座りながら考えてみるのもいいだろう。
例えば5人組のグループなら、2列と3列のシートに座ればスッキリおさまる。
7人組なら、2と2と3のシートを使用すれば、誰かが1人だけ余ることはない。
10人でも20人でも同じこと。つまり、どんな人数でも必ず仲間の誰かと座ることができるのだ。
誰か1人だけ、余ることはない。
もう少し詳しく見ていこう。
仕組みはこうだ。
2
3
4 = 2 + 2
5 = 2 + 3
6 = 3 + 3 ( 2 + 2 + 2 )
7 = 3 + 2 + 2
8 = 2 + 2 + 2 + 2 ( 3 + 3 + 2 )
・
・
・
ご覧の通り、どんな数字でも、必ず2と3の足し算で表現できるのだ。
パズルのように、2と3だけで組み合わせることができるのだ。
だから、「あれ? 吉田だけ知らないおじさんと座ってるぞー!」
とクラスメイトからからかわれる心配はいらないというわけだ。
必ず、メンバーの誰かと楽しく車内を過ごすことができる。
この2と3は両方とも「素数」だ。
素数とは、2 , 3, 5 , 7 …… という風に、自分の数でしか割れない数のこと(1は含めない)。
例えば、「4」だと、自分の数である「4」でも割れるが、2」でも割れてしまうので却下。
素数の2と3はなかなかに優秀な数字なのだ。
必ず、どんな団体でもうまくグループ分けを行い、速やかに座席を均等に分配することができるからだ。まるで、優秀なホテルの案内係のように「こちらへどうぞ」と案内してくれる。
「それでしたら、このパターンでお座りください」
スマートに、軽やかに、座席がうまっていく。
「いらっしゃいませ」
ところで、素数定規というものをご存知だろうか。
世の中にある不便を研究する、「不便益システム研究所」という所が開発した定規だ。
名前の通り、素数に関係した定規となっている。
つまり、素数の所にしかメモリが記されていないのだ。
「2 , 3 , 5 , 7 , 11 , 13 , 17 」にしか、メモリと数字が打たれていないのだ。
それ以外は何もない。
竹でできたシンプルな定規だ。
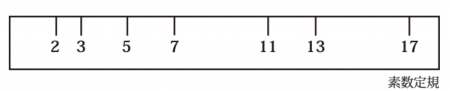
そして、不便を研究するグループが作っただけに、本当に不便なのだ。不便極まりないのだ。
なぜって、素数分しか測ることができないのだから。
ただ、開発者の言い分としてはこうだ。
「だって、2と3があるじゃない。 何センチでも測ることはできるよ」
そう、新幹線のシートのように、2と3が存在しているのだ。したがって、その数字を駆使すれば、必要な長さは計測可能というわけ。かなり小刻みにはなるが、20センチでも、30センチでも、1メートルでも、測ることはできるという仕組みだ。
ただ、不便ではあるが。
急いでいる時に長さを測ろうものなら、メモリが変な所にしかないので「あーもう!!」となる。イラッとする。思わず「不便だなー!」と言ってしまう。
さて、数学というものは案外と私たちの生活に潜んでいるものらしい。
新幹線の座席に素数が使われているなど、誰が想像しただろうか。
「へーそうなんだ!」
そう思っていただければ幸いである。
意外な所で活用されている数学。
「素数なんて、世の中で使わないよ」
そんなことを口にしたことのある人も、この機会にちょっと素数を見直してほしい。
次に新幹線に乗る機会がある時は、座席を見ながら素数というものを少しだけでも感じてみてほしい。
「ほうほう、この2れつと3列が素数なんだね」
目の前の世界がちょっとスパイシーになるはず。ワンテイスト。小さな彩り。
ほんの少し、世の中の見え方が変わるかもしれない。
❏ライタープロフィール
吉田 健介(READING LIFE 編集部公認ライター)
現役の中学校教師。教師が一方的に話をするのではなく、生徒同士が話し合いながら課題を解決していく対話型の授業を行なっている。様々な研究授業で自らの授業を公開。生徒が能動的に学習できるような授業づくりを目指している。
この記事は、天狼院書店の大人気講座・人生を変えるライティング教室「ライティング・ゼミ」を受講した方が書いたものです。ライティング・ゼミにご参加いただくと記事を投稿いただき、編集部のフィードバックが得られます。チェックをし、Web天狼院書店に掲載レベルを満たしている場合は、Web天狼院書店にアップされます。
★10月末まで10%OFF!【2022年12月開講】人生を変えるライティング教室「天狼院ライティング・ゼミ《土曜コース》」



