6. 改めてサンキュー 〜直角三角形〜《オトナのための中学数学》

記事:吉田健介(READING LIFE編集部公認ライター)
人はボーッとしたり、リラックスしている状態に、いいアイデアが浮かびやすくなるそうだ。窓の外を眺めたり、湯船に浸かりながら壁のシミを見たり、風に揺れる葉っぱに目を任せていたり。
ある研究によると、アイデアが浮かんだ70%は、シャワーを浴びている時という話がある。とにかく、脳をスリープモードにすると、静かな池に釣り糸を垂らすように、休日のキャンプのようなのどかな気分になり、大物が釣れやすくなるみたいだ。音量のつまみを下げるように、周りを静かにし、気持ちを一旦落ち着かせて脳に静寂を与える。そうすることで、いいアイデアが湧いてきやすいということだろう。
ピタゴラスもそんなリラックスモードだったのかもしれない。この定理を思い付いたのは、散歩をしながら、床のタイルを見ている時だったそうだ。頭を整理するために一旦外へ出たのか、または忘れ物を取りに出かける最中だったのか。ボーっとしながら、床に張り巡らされた模様を見つつ、1つの定理を発見したのだ。
「……ん?」
最初は、目の前を魚が通り過ぎたくらいの感覚だっただろう。些細なこと。魚とも認識はしていなかったかも。少ししてから、「今のは何だ?」という程度。
やがて、通り過ぎたのが魚であることを認識する。
やがて、どれくらいの大きさだったのか、どのくらいの速さだったのかを思い返す。
やがて、分析を始める。
脳内には色々な部分からアクセスを求められる。コードが一箇所に集中。ピピピッ
情報分析。現象のスキャン。
「……直角三角形って……」
ピタゴラスの定理が生まれた瞬間。
当時、シャワーがあったら、ピタゴラスはもっとたくさんの、もっとすごい発見をしていたのかもしれない。ただ、間違いなく彼はリラックス状態にあり、肩の力を抜いて、1つの定理を見つけたのだ。現代でも活用される定理になろうとは思いもせずに。
「中学校で習った数学、何か覚えている?」
そう質問されたら何と答えるだろうか。
ピタゴラスの定理、別名、三平方の定理は、トップ3に入ってくる有名どころではないだろうか。
他にもいろいろなことを教わったはずなのに、自然と口から出てしまう定理。妙に記憶に残っている公式。
形はシンプルだ。
定理に使用されている記号は難しくない。
パッと見ただけで、どういったことを意味しているのかが分かりやすいし、長くもない。
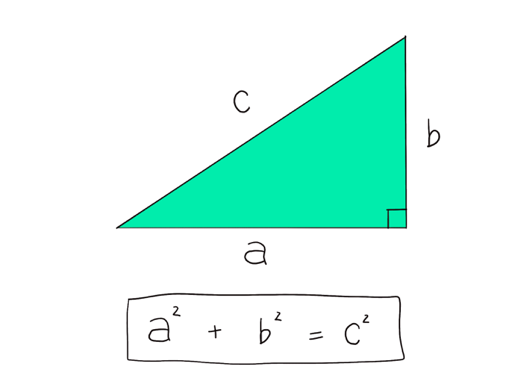
「あれ、外国の人だ」と思うように、外見的な特徴から判断しやすい。親しみやすい公式。
さて、ではこのピタゴラスの定理はどのような場面で使われているのだろうか。
何となく「どこかには使われているでしょ」と想像は付きやすいだろう。三角形であることが、共感を呼びやすいポイントであるからだ。
ただ、具体的にどの場面で使用されているかまでは…… そういった人がほとんどかもしれない。
ピタゴラスの定理は、三角形、中でも直角三角形にまつわる定理だ。
直角三角形といえば、90°がくっついていることが大きな特徴。
90°、垂直、水平、真っ直ぐ……
こうした特徴から、建築でよく使われている。
例えば、対象物までの距離を測りたいとき。
「あの人たち、何してるんだろう?」
道を歩いているとき、カメラの三脚のようなものを立てて、何かをしている人を見たことはないだろうか。
何かを測っているんだろうな…… くらいは分かるが、具体的に何をしているか分からない、一体何を測っているの? という人たち。
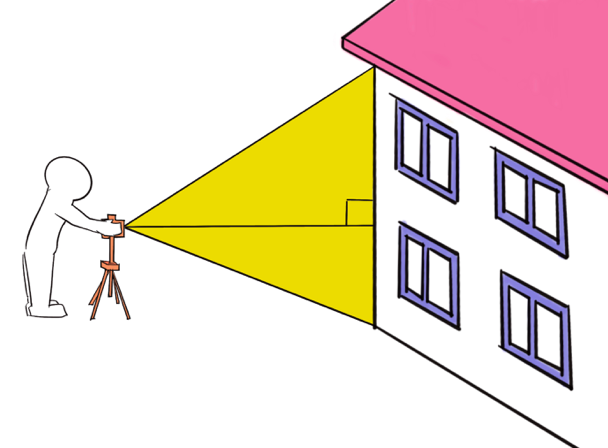
予想通り何かを測っているわけだが、あの機械、建築の現場でよく使われるものだ。直角三角形をうまく活用して、目標物までの角度や距離を測っている。あの機械を使えば、様々なものを正確に測ることができる。
1つ例を挙げてみよう。下図のように、窓の高さだけを知りたいとする。測定機から飛ばされたレーザーで、水平距離を測定(AB)。続いて、窓の上に向かって、距離を測定(AC)。すると、1つの直角三角形を作ることができる。△ABCだ。これで、ピタゴラスの定理を使ってBCの高さが計算できる。
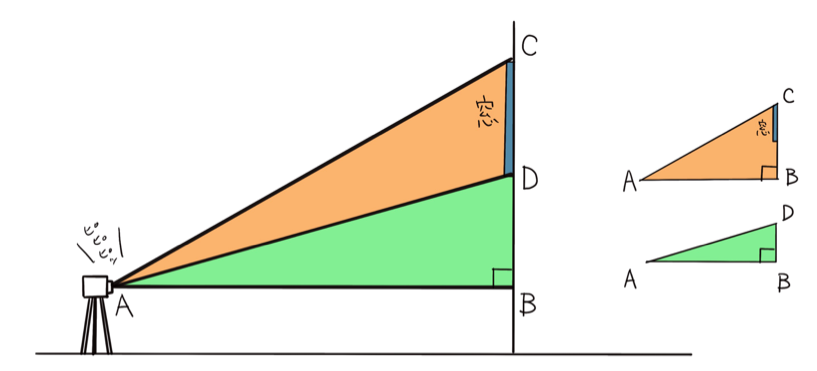
続いて、窓の下に向かって、もう1本距離を測定(AD)。これで新たに直角三角系△ABDができる。同じように、ピタゴラスの定理から、BDを計算で求める。そして、先ほどのBCとの差で、窓の高さが判明するわけだ。
ところで、直角三角形の特徴から、手作業で90°を測ることができる。長さの比を使うのだ。
直角三角形にも様々な大きさが存在するわけだが、中でもきれいな数字の比で表現できる直角三角形がある。
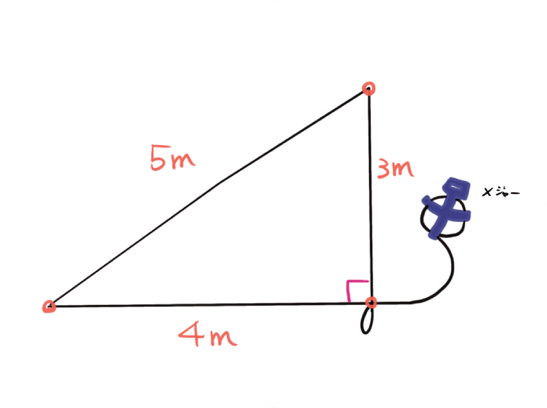
それは「 3 : 4 : 5 」
別名、「さしご」とも呼ばれており、三辺の長さの比が「 3 : 4 : 5 」となる。
「 3 : 4 : 5 」であれば、IKEAの家具を組み立てるように、直角三角形が勝手に出来上がる。
比なので、3cm、4cm、5cmでもいいし、6m、8m、10mでも構わない。とにかく「 3 : 4 : 5 」であれば、自然と直角三角形になるのだ。
そこから、更地に正方形や長方形を作りたいときは、機械を使わなくても、90°を作ることができるというわけ。日本でも昔から「さしご」は職人さんの間では定番の知識として活用されていた。
ちなみに、ピタゴラスが定理を発見するより以前、古代エジプトの時代では、「 3 : 4 : 5 」がすでに使われていた。それ以外に、「 5 : 12 : 13 」や「 15 : 8 : 17 」でも直角三角形を作ることができる。古代バビロニアや古代インドでは、すでにこうした直角三角形が発見されており、建築や観測で使用されていたことが分かっている。昔の人ってすごい。
ピタゴラスの定理にせよ、直角三角形の比にせよ、こうした知識はごく限られた人にしか使われていなかった。特別な道具。それは魔法のようなものだったに違いない。しかし今は、いつでも、誰でも、どこでも、手軽に、手早く、簡単に使うことができる。
何だか感謝。
直角三角形ってすごい。定理を発見したピタゴラスってすごい。
改めてサンキュー。
直角三角形にありがとう。
❏ライタープロフィール
吉田 健介(READING LIFE 編集部公認ライター)
現役の中学校教師。教師が一方的に話をするのではなく、生徒同士が話し合いながら課題を解決していく対話型の授業を行なっている。様々な研究授業で自らの授業を公開。生徒が能動的に学習できるような授業づくりを目指している。
この記事は、天狼院書店の大人気講座・人生を変えるライティング教室「ライティング・ゼミ」を受講した方が書いたものです。ライティング・ゼミにご参加いただくと記事を投稿いただき、編集部のフィードバックが得られます。チェックをし、Web天狼院書店に掲載レベルを満たしている場合は、Web天狼院書店にアップされます。
人生を変えるライティング教室「天狼院ライティング・ゼミ」〜なぜ受講生が書いた記事が次々にバズを起こせるのか?賞を取れるのか?プロも通うのか?〜
お問い合わせ
■メールでのお問い合わせ:お問い合せフォーム
■各店舗へのお問い合わせ
*天狼院公式Facebookページでは様々な情報を配信しております。下のボックス内で「いいね!」をしていただくだけでイベント情報や記事更新の情報、Facebookページオリジナルコンテンツがご覧いただけるようになります。
■天狼院書店「東京天狼院」
〒171-0022 東京都豊島区南池袋3-24-16 2F
TEL:03-6914-3618/FAX:03-6914-0168
営業時間:
平日 12:00〜22:00/土日祝 10:00〜22:00
*定休日:木曜日(イベント時臨時営業)
■天狼院書店「福岡天狼院」
〒810-0021 福岡県福岡市中央区今泉1-9-12 ハイツ三笠2階
TEL:092-518-7435/FAX:092-518-4149
営業時間:
平日 12:00〜22:00/土日祝 10:00〜22:00
■天狼院書店「京都天狼院」
〒605-0805 京都府京都市東山区博多町112-5
TEL:075-708-3930/FAX:075-708-3931
営業時間:10:00〜22:00
■天狼院書店「Esola池袋店 STYLE for Biz」
〒171-0021 東京都豊島区西池袋1-12-1 Esola池袋2F
営業時間:10:30〜21:30
TEL:03-6914-0167/FAX:03-6914-0168
■天狼院書店「プレイアトレ土浦店」
〒300-0035 茨城県土浦市有明町1-30 プレイアトレ土浦2F
営業時間:9:00~22:00
TEL:029-897-3325
■天狼院書店「シアターカフェ天狼院」
〒170-0013 東京都豊島区東池袋1丁目8-1 WACCA池袋 4F
営業時間:
平日 11:00〜22:00/土日祝 10:00〜22:00
電話:03−6812−1984



